Tags and keywords
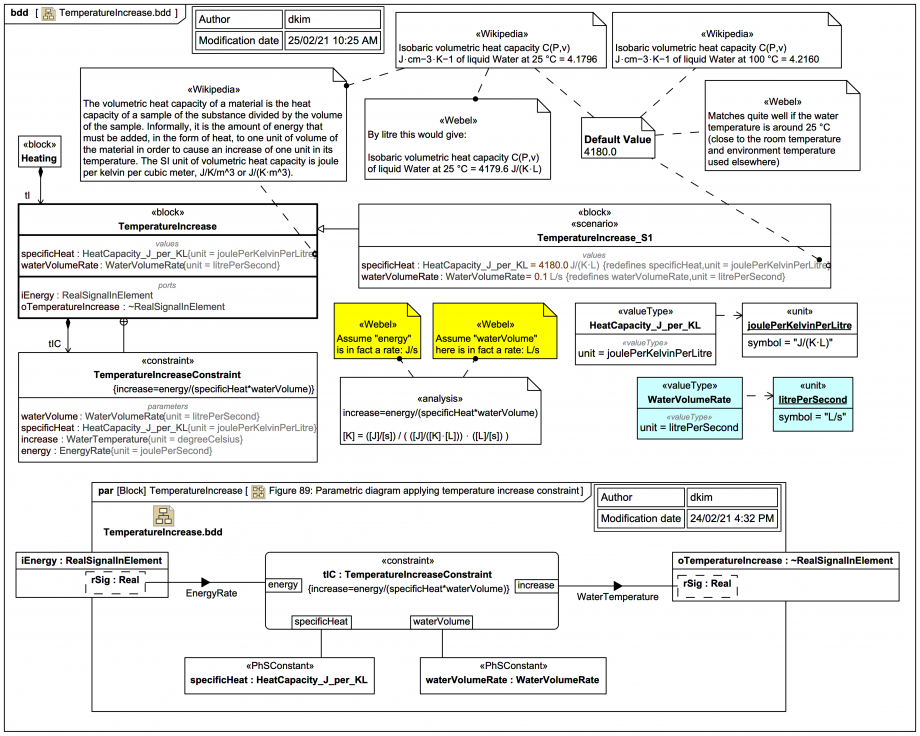
TemperatureIncrease with a supporting ConstraintBlock TemperatureIncreaseConstraint:
{increase=energy/(specificHeat*waterVolume)}
Remember this loophole?
Let's see whether we can make the numbers fit anyway:
The startup value 4180.0 for specificHeat works quite well across the expected temperature ranges if it is in J/(K⋅L), noting the following data are in J/(K⋅cm^3):
So 4180.0 J/(K⋅L) seems reasonable.
But note also that to get the dimensional analysis to work the "waterVolume" has to be a rate:
This is based in part on the observation that the consumer HeatingCalculation does NOT treat the temperature increase as a rate, together with:
Assume you've got all of the power 400 J/s from the heater (ignore any radiative loss) and plugin these values:
specificHeat -> 4.180 J/(K cm^3)
waterVolume -> 0.1 L/s
energy -> 400 J/s
L -> cm^3*1000
This gives a temperature increase of 0.956938 K. We'll see also later when we run the simulation that the assumption of waterVolume = 0.1 L/s corresponds well enough with the equivalent vapor output rate.